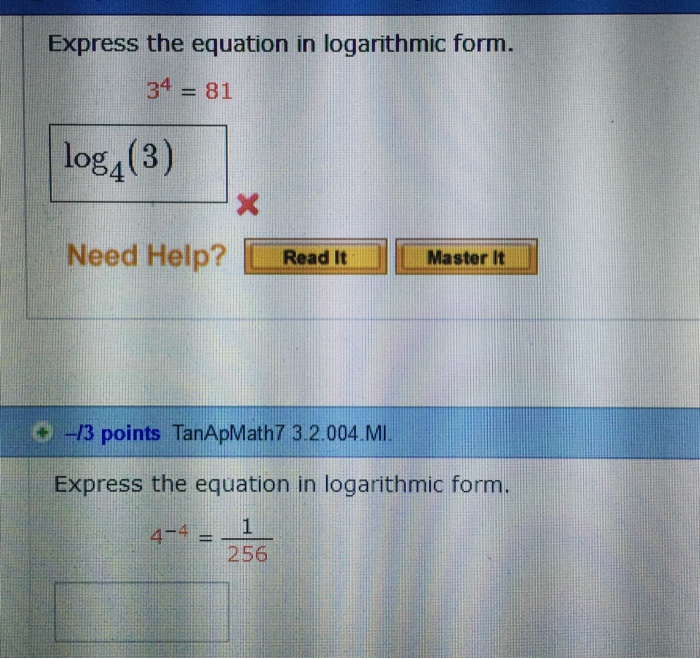
3 4 81 In Logarithmic Form
3 4 81 In Logarithmic Form - 81 = 34 = 92. ⇒log 381=log 3(3 4) ⇒log 381=4. $$\log _{81} 3=\frac{1}{4}$$ 01:26 express the given equations in logarithmic form. 34 = 81 3 4 = 81. A system of equations is a collection of two or more equations with the same set of variables. $$\log_{3}(81) = 4$$ therefore, the logarithmic form of the exponential expression $3^{4}=81$ is $\log_{3}(81) = 4$.
SOLVEDFor each statement, write an equivalent statement in logarithmic
Web how to write an exponential equation in logarithmic form. Three race to the negative. Express the following in logarithmic form: Web write in exponential form log base 3 of 81=4. Convert the exponential equation.
Solved Express the equation in logarithmic form. 3^4 = 81
Web here is the exponential equation 3 4 =81. Web how do you write 81 1 4 = 3 in logarithmic form? Math teacher · tutor for 6 years. Log 2 (8) = 3.
How to Write in Logarithmic Form
Express the following in logarithmic form: (891 votes) click here 👆 to get an answer to your question ️ 3^4=81 to logarithmic form. Web here is the exponential equation 3 4 =81. Express the following.
Logarithm Rules (aka Log Laws) Explained with Examples Maths for Kids
The logarithm of 100 to the base 10 is. Log 2 (8) = 3 2 3 = 8 log 3 (81) = 4 3 4 = 81 .
How to Write in Logarithmic Form
The number that is raised is always the subscript of log. Web [latex]{\log _3}81 = 4 \,\,\leftrightarrow\,\, {3^4} = 81[/latex] [latex]{\log _2}32 = 5 \,\,\leftrightarrow\,\, {2^5} = 32[/latex] [latex]{\log _5}125 = 3 \,\,\leftrightarrow\,\, {5^3} =.
In this case, the logarithmic expression is: The number that is raised is always the subscript of log. Here 3 is raised to the power 4 to make 81. 34 = 81 3 4 = 81. In this case, b = 3 b = 3, x = 81 x = 81, and y = 4 y = 4.
For Logarithmic Equations, Logb(X) = Y Log B ( X) = Y Is Equivalent To By = X B Y = X Such That X > 0 X > 0, B > 0 B > 0, And B ≠ 1 B ≠ 1.
What is the equivalent logarithmic form of the equation? Log 3 81 = 4 log 3 81 = 4 log 3 81 = 4 \log _{3}81=4\log _{3}81=4\log _{3}81=4 lo g 3 81 = 4 lo g 3 81 =. Log 2 (8) = 3 2 3 = 8 log 3 (81) = 4 3 4 = 81 log 5 (25) = 2 5 2 = 25 ⇒log 381=log 3(3 4) ⇒log 381=4.
Playlist Showing Steps For Logarithms And Their Graphs:
(124 votes) click here 👆 to get an answer to your question ️ a. Web how to write an exponential equation in logarithmic form. The logarithm of 100 to the base 10 is. Log3 (81) = 4 log 3 ( 81) = 4.
The Exponent Always Ends Up Being Equaled To.
B = 3 b = 3. It can be written in logarithmic form as. A system of equations is a collection of two or more equations with the same set of variables. The inverse of an exponential function is called a.
(891 Votes) Click Here 👆 To Get An Answer To Your Question ️ 3^4=81 To Logarithmic Form.
Express the following in logarithmic form: $$\log_{3}(81) = 4$$ therefore, the logarithmic form of the exponential expression $3^{4}=81$ is $\log_{3}(81) = 4$. Y = ax ⇒ logay =x ∴ 81 =34 ⇒ log381 = 4. Write the equation in its equivalent logarithmic form.
The inverse of an exponential function is called a. ⇒ log981 = log992 = 2log99 = 2. ⇒log 381=log 3(3 4) ⇒log 381=4. Web what is 81=3^4 in logarithmic form? Write the equation in its equivalent logarithmic form.